Podnoszenie liczby do kwadratu to ważna operacja matematyczna. Polega ona na pomnożeniu liczby przez samą siebie. Zapisujemy to jako $$ x^2 $$, gdzie x to dowolna liczba. Wynik tej operacji jest zawsze nieujemny, niezależnie czy mnożymy liczbę dodatnią czy ujemną. To podstawowe działanie ma wiele zastosowań w matematyce i codziennym życiu.
Kluczowe informacje:
- Kwadrat liczby to ona sama pomnożona przez siebie
- Zapis matematyczny: $$ x^2 $$
- Wynik zawsze jest nieujemny
- Działa dla liczb dodatnich, ujemnych i zera
- 0² = 0, 1² = 1, 2² = 4, 3² = 9, (-2)² = 4
Czym jest kwadrat liczby?
Kwadrat liczby to wynik mnożenia tej liczby przez samą siebie. Jest to podstawowa operacja matematyczna, zapisywana jako x², gdzie x oznacza dowolną liczbę. Obliczanie kwadratu ma kluczowe znaczenie w matematyce, znajdując zastosowanie w geometrii, algebrze i wielu dziedzinach nauki.
Wzór na obliczanie kwadratu liczby
Wzór na kwadrat liczby to: x² = x * x. W tym wzorze x reprezentuje liczbę, którą chcemy podnieść do kwadratu, a symbol * oznacza mnożenie. Na przykład, aby obliczyć kwadrat liczby 5, wykonujemy działanie: 5² = 5 * 5 = 25.
Alternatywne metody obliczania kwadratu
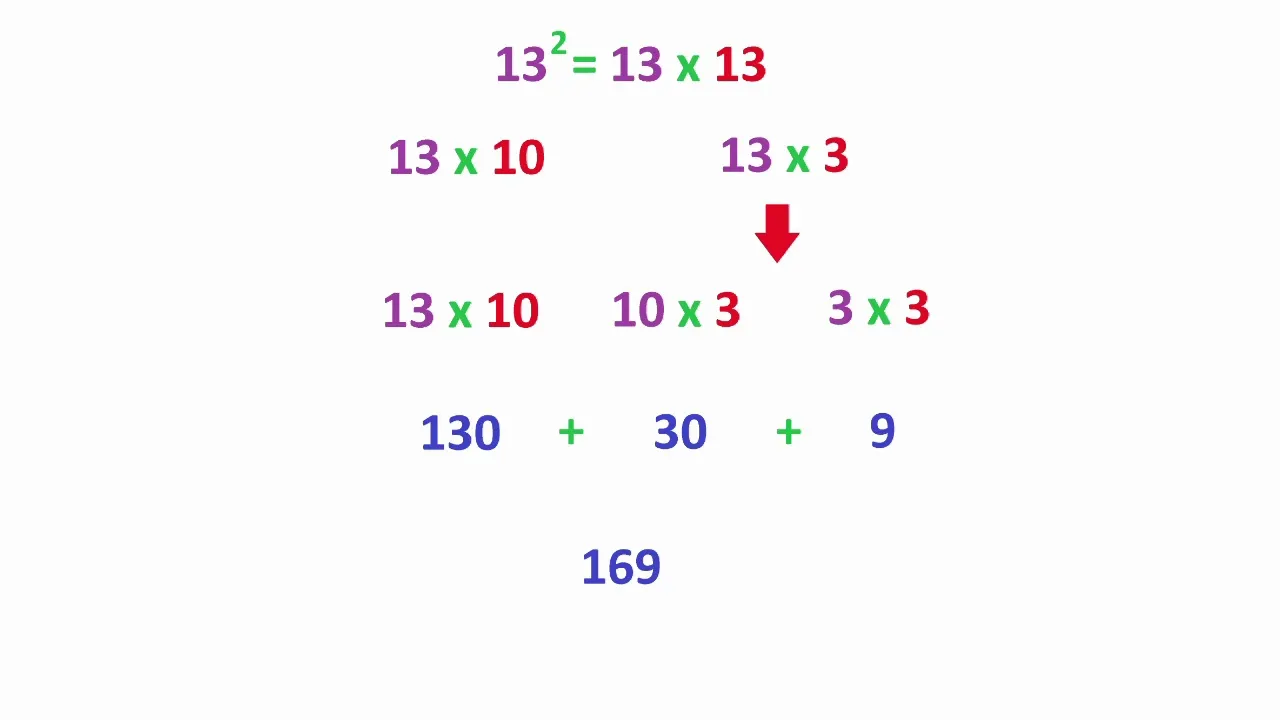
Oprócz podstawowego wzoru, istnieją inne sposoby obliczania kwadratu. Można użyć metody rozkładu na czynniki, np. (a+b)² = a² + 2ab + b², lub skorzystać z właściwości liczb, jak w przypadku liczb kończących się na 5. Te alternatywne metody mogą być szybsze w niektórych przypadkach, ale klasyczny wzór pozostaje najbardziej uniwersalny.
Czytaj więcej: Ile milimoli w molu? Poznaj dokładne przeliczenie w chemii
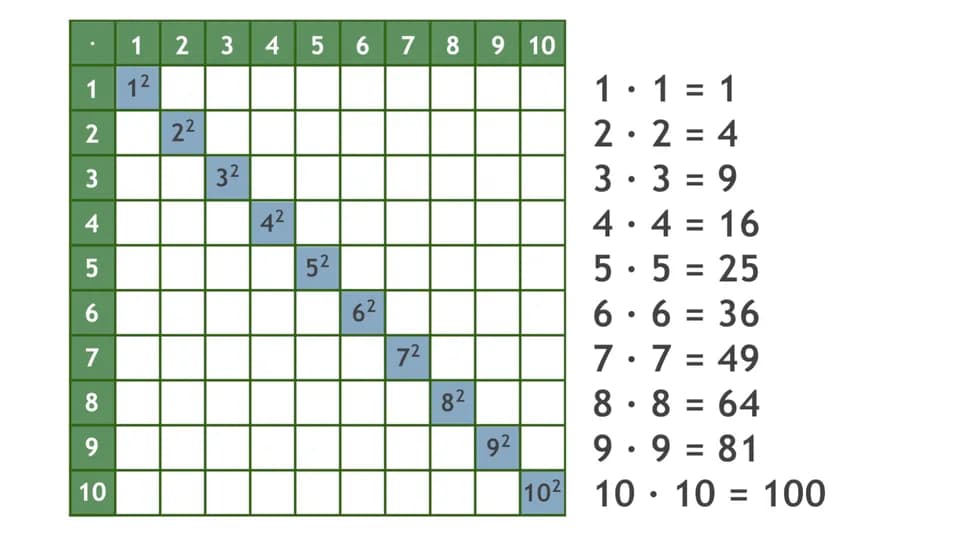
Przykłady obliczania kwadratów liczb
| Liczba | Kwadrat |
|---|---|
| 0 | 0² = 0 |
| 1 | 1² = 1 |
| 2 | 2² = 4 |
| 3 | 3² = 9 |
| 4 | 4² = 16 |
| 5 | 5² = 25 |
| 6 | 6² = 36 |
| 7 | 7² = 49 |
| 8 | 8² = 64 |
| 9 | 9² = 81 |
| 10 | 10² = 100 |
Analizując powyższe wyniki, zauważamy, że kwadraty liczb rosną coraz szybciej. Ta progresja jest kluczowa w wielu zagadnieniach matematycznych i naukowych.
Kwadraty liczb ujemnych
Przy podnoszeniu do kwadratu liczb ujemnych, wynik zawsze jest dodatni. Na przykład, (-3)² = 9, tak samo jak 3². To pokazuje, że kwadrat liczby jest niezależny od jej znaku.Właściwości kwadratów liczb
- Nieujemność: Kwadrat każdej liczby rzeczywistej jest nieujemny.
- Monotoniczność: Dla liczb dodatnich, większa liczba ma większy kwadrat.
- Parzystość: Kwadrat liczby parzystej jest parzysty, a nieparzystej - nieparzysty.
- Odwracalność: Pierwiastek kwadratowy z kwadratu liczby daje wartość bezwzględną tej liczby.
- Addytywność: Kwadrat sumy dwóch liczb nie równa się sumie ich kwadratów.
Dlaczego kwadrat liczby jest zawsze nieujemny?
Kwadrat liczby jest zawsze nieujemny, ponieważ mnożymy liczbę przez samą siebie. Niezależnie od tego, czy mnożymy dwie liczby dodatnie czy dwie ujemne, wynik zawsze będzie dodatni. Ta właściwość ma kluczowe znaczenie w wielu dziedzinach nauki i techniki.
Zastosowania kwadratów liczb w życiu codziennym
Obliczanie kwadratu znajduje zastosowanie w architekturze przy projektowaniu powierzchni, w fizyce przy obliczaniu energii kinetycznej, czy w finansach przy kalkulacji zysków. W nauce i technice kwadraty są niezbędne do analizy danych, optymalizacji procesów i modelowania zjawisk fizycznych.
Dla liczb kończących się na 5, kwadrat to 25 plus kwadrat pierwszej cyfry razy 100. Dla liczb bliskich 10 lub 100, użyj wzoru (a+b)(a-b) = a² - b². Ćwicz te triki, a obliczanie kwadratów stanie się łatwiejsze!
Ciekawostki związane z kwadratami liczb
- Liczby pierwsze: Istnieją liczby pierwsze będące sumą dwóch kwadratów.
- Kwadrat magiczny: To tablica liczb, gdzie sumy w wierszach, kolumnach i przekątnych są równe.
- Twierdzenie Pitagorasa: Opiera się na kwadratach długości boków trójkąta prostokątnego.
- Paradoks Bertranda: Dotyczy prawdopodobieństwa w kwadracie, pokazując niejednoznaczność w teorii prawdopodobieństwa.
Podsumowanie: Dlaczego warto znać kwadraty liczb?
Znajomość kwadratów liczb usprawnia rozwiązywanie problemów matematycznych, pomaga w szacowaniu i analizie danych oraz rozwija umiejętność szybkich obliczeń. To fundamentalna wiedza, przydatna w nauce, pracy i życiu codziennym. Regularnie ćwicz obliczanie kwadratów, aby rozwijać swoje umiejętności matematyczne!
Kwadraty liczb: klucz do matematycznej sprawności i praktycznych zastosowań
Obliczanie kwadratu liczby to fundamentalna umiejętność matematyczna, która otwiera drzwi do głębszego zrozumienia wielu koncepcji i zjawisk. Od prostego wzoru x² = x * x, przez alternatywne metody obliczeniowe, aż po fascynujące właściwości i ciekawostki - kwadraty liczb są wszechobecne w matematyce i codziennym życiu.Zrozumienie, dlaczego kwadraty są zawsze nieujemne i jak zachowują się dla liczb ujemnych, pozwala nam lepiej pojąć naturę liczb i operacji matematycznych. Praktyczne zastosowania, od architektury po fizykę i finanse, pokazują, jak ta prosta koncepcja przenika różne dziedziny nauki i techniki.
Rozwijanie umiejętności szybkiego obliczania kwadratów, korzystanie z trików obliczeniowych i poznawanie fascynujących ciekawostek nie tylko usprawnia nasze zdolności matematyczne, ale także poszerza horyzonty myślenia. Pamiętajmy, że regularne ćwiczenie tej umiejętności to inwestycja w naszą matematyczną sprawność i zdolność rozwiązywania problemów w różnych aspektach życia.