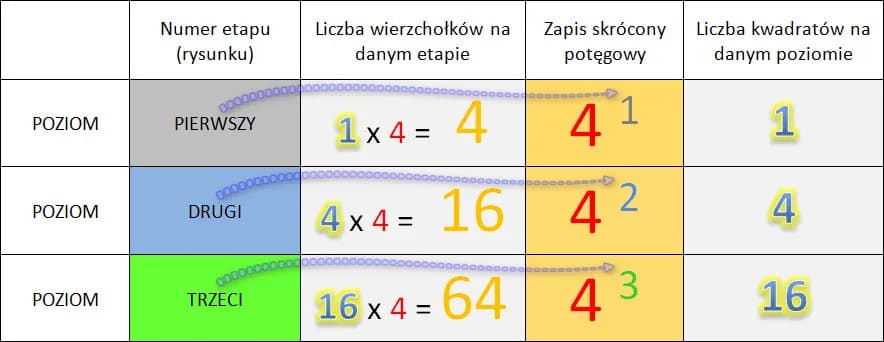
Wyrażenie $$ x \times x $$ jest równoważne $$ x^2 $$. To ważne pojęcie w matematyce. Mnożenie liczby przez samą siebie daje jej kwadrat. Funkcja kwadratowa ma ciekawe właściwości. Jej wykres to parabola. Ma minimum w punkcie zero. Domena to wszystkie liczby rzeczywiste. Zakres to liczby nieujemne.
Kwadrat liczby ma zastosowania w wielu dziedzinach. Pojawia się w geometrii, fizyce i statystyce. Zrozumienie tej koncepcji pomaga w rozwiązywaniu problemów matematycznych. Najważniejsze informacje:- $$ x \times x = x^2 $$ to definicja kwadratu liczby
- Wykres funkcji kwadratowej to parabola
- Minimum funkcji to punkt (0,0)
- Domena to R, zakres to [0,∞)
- Pochodna funkcji kwadratowej to $$ f'(x) = 2x $$
- Całka z $$ x^2 $$ to $$ \frac{x^3}{3} + C $$
Definicja kwadratu liczby
Kwadrat liczby to wynik mnożenia liczby przez samą siebie. X razy x oznacza właśnie operację podnoszenia liczby do kwadratu. To podstawowe pojęcie w matematyce, kluczowe dla zrozumienia wielu bardziej zaawansowanych koncepcji. Przykładowo, kwadrat liczby 5 to 25.
Zapis matematyczny kwadratu
X razy x zapisujemy jako x^2. Ta notacja to skrócony sposób przedstawienia potęgowania, gdzie liczba jest mnożona przez siebie określoną liczbę razy. W przypadku kwadratu, mnożymy liczbę przez siebie dwukrotnie.
- x * x = x^2
- x² (zapis z użyciem indeksu górnego)
- x do kwadratu (zapis słowny)
Czytaj więcej: Ile to 30 cm? Poznaj przeliczniki i praktyczne zastosowania
Jak obliczyć kwadrat liczby?
Najprostszą metodą obliczenia kwadratu liczby jest jej pomnożenie przez samą siebie. Na przykład, aby znaleźć kwadrat 7, mnożymy 7 * 7. Alternatywnie, możemy użyć potęgowania, zapisując 7^2, co daje ten sam wynik.
| Liczba | Kwadrat |
|---|---|
| 1 | 1 |
| 2 | 4 |
| 3 | 9 |
| 4 | 16 |
| 5 | 25 |
| 6 | 36 |
| 7 | 49 |
| 8 | 64 |
| 9 | 81 |
| 10 | 100 |
Kwadraty liczb ujemnych
Przy podnoszeniu do kwadratu liczb ujemnych, wynik zawsze jest dodatni. Dzieje się tak, ponieważ mnożymy dwie liczby o tym samym znaku. Przykładowo, kwadrat liczby -5 to również 25.
Dlaczego kwadrat jest zawsze nieujemny?
Kwadrat liczby jest zawsze nieujemny ze względu na właściwości mnożenia. Gdy mnożymy dwie liczby o tych samych znakach (dodatnie lub ujemne), wynik jest zawsze dodatni. Dla zera, kwadrat również daje zero. Na wykresie funkcji kwadratowej widać to jako parabolę, która nigdy nie schodzi poniżej osi X.
Zastosowania kwadratu w życiu codziennym
Kwadrat liczby ma wiele praktycznych zastosowań:
- Obliczanie pola powierzchni: np. pokoju o wymiarach 4x4 m
- Fizyka: obliczanie przebytej drogi w ruchu jednostajnie przyspieszonym
- Finanse: obliczanie odsetek składanych
- Statystyka: obliczanie odchylenia standardowego
- Technologia: kompresja danych w formacie JPEG
Kwadrat w geometrii
W geometrii, kwadrat liczby jest ściśle związany z polem kwadratu jako figury geometrycznej. Pole kwadratu o boku długości a wynosi a^2. Przykładowo, kwadrat o boku 5 cm ma pole 25 cm².
Związek kwadratu z pierwiastkiem kwadratowym
Pierwiastek kwadratowy to operacja odwrotna do podnoszenia do kwadratu. Oznacza liczbę, która pomnożona przez siebie daje daną wartość. Relacja między kwadratem a pierwiastkiem jest symetryczna: jeśli a² = b, to √b = a. Na przykład, pierwiastek z 25 to 5, ponieważ 5² = 25.
Kwadraty w algebrze
Wzory skróconego mnożenia to narzędzia algebraiczne wykorzystujące właściwości kwadratów. Najbardziej znany to (a+b)² = a² + 2ab + b². Stosując go, możemy szybko obliczyć np. (10+3)² = 10² + 2*10*3 + 3² = 100 + 60 + 9 = 169.
Rozkład na czynniki kwadratowe
Rozkład na czynniki kwadratowe to proces odwrotny do rozwijania kwadratu sumy. Polega na przedstawieniu wyrażenia w postaci iloczynu dwóch nawiasów. Przykładowo, x² + 6x + 9 można rozłożyć na (x+3)².
Funkcja kwadratowa
Funkcja kwadratowa to funkcja postaci f(x) = ax² + bx + c, gdzie a≠0. Jej wykres to parabola, która może być otwarta w górę (a>0) lub w dół (a<0). Współczynnik a wpływa na szerokość paraboli, b na jej przesunięcie w poziomie, a c na przecięcie z osią Y.
Wierzchołek paraboli
Wierzchołek paraboli to punkt, w którym funkcja osiąga ekstremum (minimum dla a>0, maksimum dla a<0). Jego współrzędne można obliczyć ze wzorów: x = -b/(2a) dla x, oraz y = f(x) po podstawieniu obliczonego x.
Kwadrat liczby: Kluczowe koncepcje i zastosowania
Kwadrat liczby to fundamentalne pojęcie matematyczne, które ma szerokie zastosowanie w różnych dziedzinach. Od prostego mnożenia liczby przez samą siebie, poprzez zapis x^2, aż po skomplikowane funkcje kwadratowe - zrozumienie tej koncepcji otwiera drzwi do głębszego poznania matematyki.
Warto pamiętać, że kwadrat liczby zawsze daje wynik nieujemny, co ma istotne implikacje w geometrii i algebrze. Znajomość właściwości kwadratów pomaga w rozwiązywaniu problemów związanych z polami powierzchni, ruchem jednostajnie przyspieszonym czy analizą statystyczną danych.
Związek między kwadratem a pierwiastkiem kwadratowym, a także zastosowanie kwadratów w wyrażeniach algebraicznych, pokazuje, jak głęboko ta koncepcja jest zakorzeniona w matematyce. Zrozumienie funkcji kwadratowej i jej wykresu - paraboli - stanowi podstawę do analizy wielu zjawisk w świecie rzeczywistym, od trajektorii rzuconych obiektów po optymalizację procesów biznesowych.