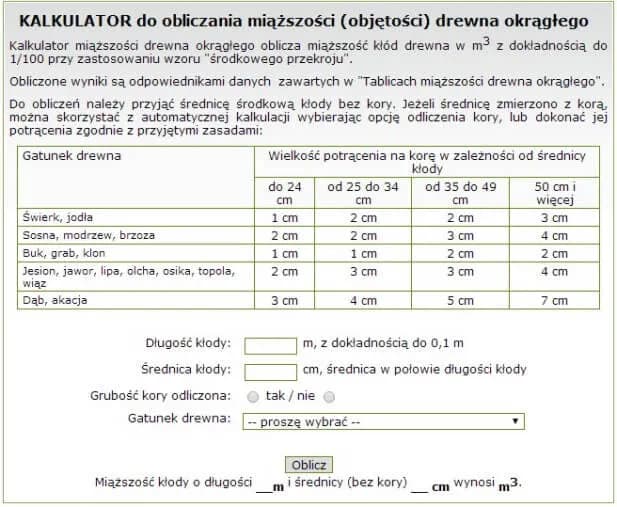
Przeliczanie metrów kwadratowych (m²) na metry sześcienne (m³) wymaga uwzględnienia wysokości obiektu. To kluczowe, bo m² to miara powierzchni, a m³ objętości. Bez znajomości wysokości nie da się dokonać dokładnego przeliczenia.
Podstawowa zasada: 1 m³ = 1 m² × 1 m wysokości. Czyli metr sześcienny to objętość prostopadłościanu o podstawie 1 m² i wysokości 1 m. Chcąc przeliczyć dowolną powierzchnię na objętość, mnożymy ją przez wysokość. Najważniejsze informacje:- Przeliczenie m² na m³ wymaga znajomości wysokości
- Wzór: Objętość (m³) = Powierzchnia (m²) × Wysokość (m)
- 1 m² przy wysokości 1 m daje 1 m³
- Ta sama powierzchnia przy innej wysokości da inną objętość
- Bez informacji o wysokości przeliczenie jest niemożliwe
Różnica między jednostkami powierzchni a objętości
Metr kwadratowy (m²) to jednostka miary powierzchni. Reprezentuje ona obszar kwadratu o bokach długości 1 metra. Z kolei metr sześcienny (m³) to jednostka objętości, oznaczająca przestrzeń zajmowaną przez sześcian o krawędziach długości 1 metra.
Kluczowe różnice między tymi jednostkami wynikają z ich wymiarowości. M² odnosi się do dwuwymiarowej przestrzeni, opisując płaskie powierzchnie, takie jak podłogi czy ściany. Natomiast m³ dotyczy przestrzeni trójwymiarowej, uwzględniając również wysokość, co jest istotne przy obliczaniu objętości pomieszczeń czy zbiorników.
Wzór na przeliczanie m² na m³
Wzór na przeliczanie m² na m³ to: Objętość (m³) = Powierzchnia (m²) × Wysokość (m). Każdy element tego równania ma kluczowe znaczenie. Powierzchnia stanowi podstawę obliczenia, wysokość dodaje trzeci wymiar, a ich iloczyn daje nam objętość. Ten prosty wzór pozwala łatwo przekształcić 1m2 w m3, dodając informację o wysokości.
Czytaj więcej: Ile to jest godzin? Poznaj podstawowe informacje o czasie
Dlaczego wysokość jest kluczowa w obliczeniach?
Wysokość odgrywa kluczową rolę w przeliczaniu m2 na m3. Bez niej niemożliwe jest określenie objętości, ponieważ sama powierzchnia nie daje pełnego obrazu przestrzeni. To właśnie wysokość przekształca płaski obszar w bryłę, umożliwiając obliczenie jej objętości. Zmiana wysokości przy stałej powierzchni drastycznie wpływa na końcowy wynik obliczeń.
- Wysokość dodaje trzeci wymiar, przekształcając powierzchnię w objętość
- Umożliwia precyzyjne określenie rzeczywistej przestrzeni
- Pozwala na porównywanie różnych przestrzeni o tej samej podstawie
Jak zmiana wysokości wpływa na wynik?
Zmiana wysokości ma bezpośredni i proporcjonalny wpływ na obliczaną objętość. Podwojenie wysokości oznacza podwojenie objętości, a zmniejszenie jej o połowę skutkuje zmniejszeniem objętości o 50%. Ta zależność pozwala na szybkie szacowanie zmian objętości przy modyfikacjach wysokości.
| Powierzchnia (m²) | Wysokość (m) | Objętość (m³) |
|---|---|---|
| 1 | 1 | 1 |
| 1 | 2 | 2 |
| 1 | 3 | 3 |
| 1 | 4 | 4 |
| 1 | 5 | 5 |
Praktyczne przykłady obliczeń
Przykład 1: Objętość pokoju. Załóżmy, że mamy pokój o powierzchni 20 m² i wysokości 2,5 m. Aby obliczyć jego objętość, mnożymy: 20 m² × 2,5 m = 50 m³. Oznacza to, że pokój ma objętość 50 metrów sześciennych, co jest istotne np. przy planowaniu wentylacji.Przykład 2: Objętość basenu. Basen ma powierzchnię 50 m² i głębokość 1,5 m. Przeliczając m2 na m3, otrzymujemy: 50 m² × 1,5 m = 75 m³. Taka objętość pozwala określić, ile wody potrzeba do napełnienia basenu oraz jakie będą koszty jej uzdatniania.
Najczęstsze błędy przy przeliczaniu jednostek
- Pomijanie jednostek w obliczeniach, co prowadzi do nieprawidłowych wyników
- Mylenie m² z m³ w kontekście zastosowań
- Nieuwzględnianie wysokości przy przeliczaniu powierzchni na objętość
- Błędne zaokrąglanie wyników, co może prowadzić do znaczących niedokładności
Zastosowania w życiu codziennym
Umiejętność przeliczania 1m2 na m3 jest niezwykle przydatna przy remontach. Pozwala dokładnie obliczyć ilość potrzebnej farby do pomalowania ścian, uwzględniając ich wysokość. Dzięki temu unikamy kupowania zbyt dużej lub zbyt małej ilości materiałów.
W ogrodnictwie, zamiana jednostek powierzchni na objętość pomaga w planowaniu nawadniania. Znając powierzchnię ogrodu i wymaganą głębokość nawodnienia, możemy precyzyjnie określić ilość potrzebnej wody, co przekłada się na oszczędności i efektywne zarządzanie zasobami.
Przy zakupie mebli, szczególnie szaf czy regałów, przeliczanie m2 na m3 pozwala ocenić, ile rzeczy zmieści się w danym meblu. Porównując objętość mebla z objętością posiadanych przedmiotów, łatwiej dobrać odpowiedni rozmiar i uniknąć zakupu zbyt małego lub zbyt dużego mebla.
Wykorzystanie w budownictwie i architekturze
W projektowaniu budynków, przeliczanie m2 na m3 jest kluczowe dla określenia kubatury pomieszczeń. Pozwala to na precyzyjne planowanie systemów ogrzewania, klimatyzacji i wentylacji, zapewniając komfort użytkownikom i optymalizując koszty eksploatacji.
W branży budowlanej, umiejętność zamiany jednostek powierzchni na objętość jest niezbędna przy szacowaniu ilości materiałów. Dotyczy to m.in. obliczania ilości betonu potrzebnego do zalania fundamentów, ilości izolacji termicznej czy akustycznej. Precyzyjne obliczenia pomagają uniknąć marnotrawstwa materiałów i optymalizują koszty budowy.
Narzędzia ułatwiające obliczenia
Popularne kalkulatory online, takie jak "Omni Calculator" czy "Calculator.net", oferują proste narzędzia do przeliczania m2 na m3. Większość z nich pozwala na wprowadzenie powierzchni i wysokości, automatycznie obliczając objętość. Niektóre oferują dodatkowe funkcje, jak przeliczanie między różnymi jednostkami miary.
Korzystanie z automatycznych narzędzi znacznie przyspiesza proces obliczeń. Eliminuje też ryzyko błędów matematycznych, co jest szczególnie istotne przy skomplikowanych lub wielokrotnych obliczeniach.
Kluczowe aspekty przeliczania m² na m³ - od teorii do praktyki
Przeliczanie 1m2 na m3 to fundamentalna umiejętność w wielu dziedzinach życia. Zrozumienie różnicy między powierzchnią a objętością oraz roli wysokości w tych obliczeniach otwiera drzwi do precyzyjnego planowania przestrzeni, efektywnego zarządzania zasobami i optymalizacji kosztów w budownictwie, architekturze czy codziennym życiu.
Kluczem do sukcesu jest pamiętanie o prostym wzorze: Objętość (m³) = Powierzchnia (m²) × Wysokość (m). Ta formuła, choć nieskomplikowana, ma ogromne znaczenie praktyczne. Pozwala na dokładne obliczenia objętości pomieszczeń, ilości potrzebnych materiałów budowlanych czy nawet wody do napełnienia basenu.Warto pamiętać, że zamiana jednostek powierzchni na objętość znajduje zastosowanie w wielu codziennych sytuacjach - od remontów i zakupów mebli po planowanie ogrodu. W profesjonalnym kontekście, umiejętność ta jest niezbędna dla architektów, inżynierów i budowlańców. Wykorzystanie nowoczesnych narzędzi, takich jak kalkulatory online, może znacznie ułatwić i przyspieszyć proces obliczeń, minimalizując ryzyko błędów.